| < Previous page | Next page > |
HillsideShallow Landslide Density - Hillside
Parameter Description: Shallow landslide density is based on an empirically calibrated model of Generic Erosion Potential linked to landslide density (number/area). The model focuses on shallow failures (approximately less than 6 feet deep), typically underlain by bedrock, where vegetation rooting strength and pore water pressure are important components. Based on Miller and Burnett (2007). To apply the tools, see Figures 3 through 5.
There are three model components: (1) shallow landslide potential with delivery to streams not considered, (2) shallow landslide intensity in which deliver of sediment and organic debris to streams is considered, and (3) a calculation of landslide (intensity) risk proportion (identifying areas responsible to certain percentiles of landslide risk across the watershed (starting with the most unstable), such as the top 20%, the next 20% and so on. Note that in the context of sediment delivery, a user may define the channel gradient threshold that governs delivery, e.g., a delivery threshold of less than or equal to 20% will reveal more areas that can deliver compared to a delivery threshold of 10% (see Delivery Tool).
Important Notice: This erosion model is calibrated for the Oregon Coast Range. Thus when used outside of that landscape, the model should be considered as a screening tool that provides a relative ranking of instability potential(e.g., low - high). Although the model employs universal topographic indicators of shallow landslide potential increased accuracy and resolution can be obtained when shallow landslide density model is calibrated using local data (georeferenced locations of landslides or gullies). A landslide calibration tool is planned for NetMap in later 2014. Also see Warning about using Slope Stability Models.
Data Type: Grid
Grid Name: LSDEN_GRID; Common name: Landslide
Grid Name: LS_DEL_GRID; Common name: Landslide-delivery
Common name: Shallow Landslide Source Proportion; TOC name: Landslide_Proportions; Grid Name: srcprop_id.flt;
TOC = Arc Table of Contents
Units: multiple of a landscape mean landslide density (number/km2);values range from 1 (the mean number of landslides/square kilometer) to 13; proportion (percentage 0 - 100%) of landslide risk, starting with the highest (Source Proportion)
NetMap Module/Tool: Erosion Module/Shallow Landslide Potential; River Builder (pre run, loaded)
Model Description (all model components):
Calculation of shallow landslide potential, in terms of landslide intentisy (density), utilizes a spatially distributed topographic weighting term (see Generic Erosion Potential or GEP) multiplied by a mean landslide density for the region (Miller and Burnett 2007a). The topographic weighting term is determined from locations of landslides mapped in the Oregon Coast Range (Robison et al. 1999). The mean landslide density uses a constant value of 1.0 simply to show intrinsic spatial differences in topographic controls on landslide locations. Topographic weighting ‘w’ is based on the relative density of landslide points found within a specified range of a topographic attribute, such as slope gradient:
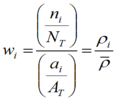 Here wi is the topographic weighting to apply to the ith range of topographic values (e.g., the ith class for values binned into specified classes), ni is the number of landslides mapped within that range of topographic values, NT is the total number of landslides mapped over the study area, ai is the area encompassing that range of topographic values, and AT is the total area of the study site. As indicated, w is a relative landslide density, i.e., the density (rI = ni/ai) of points within a specified range of topographic attribute values divided by the total mean density. The parameter focuses on slope steepness and hillslope curvature or convergence (Figure 1).
 Figure 1. Steep and convergent topography is the target of NetMap’s shallow landslide intensity model. (A) Gully in a post fire landscape in Idaho and shallow failures in bedrock hollows in coastal Oregon (also following a fire).
We calculate a topographic weighting value for every DEM pixel. Multiplied by a specified mean landslide density, it gives a spatially distributed measure of landslide density, in a parameter called ‘Landslide’ (Attribute name = LS_GRID). Integrated over area, or summed over DEM pixels, the relative index of landslide density provides an estimate of how many landslides would be mapped (based on the specified mean landslide density) over any specified area (Figure 2).
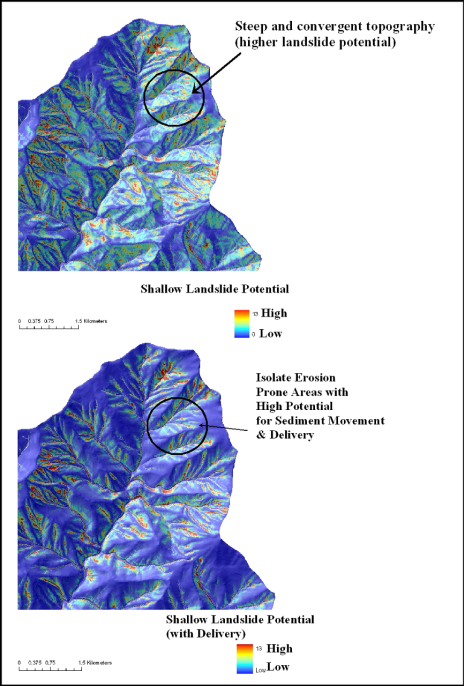 Figure 2. Shallow landslide potential with delivery (bottom) confines those steep and convergent areas most likely to deliver sediment to streams and offers more site specificity for isolating potential erosion areas.
Model Description (1/3): Shallow Landslide Potential;
Field Name: LS_GRID; Common name: Landslide
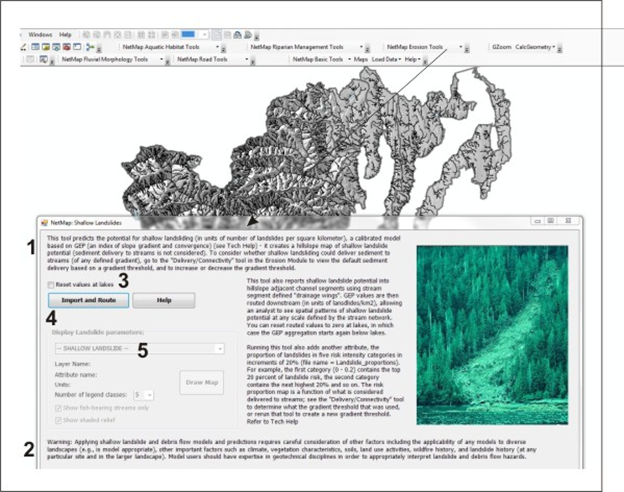 Figure 3. NetMap's Shallow Landslide potential tool uses an index of hillslope gradient and convergence and is calibrated to Oregon Coast Range data (1); it is appropriate in any landscape prone to shallow landsliding, although as a relative index. Use of the tool is best done by analysts with some background in slope stability (2). When first running this tool in a watershed, a user decides to "reset values at lakes" (3) in the channel based attribute of the Shallow Landslide Intensity (e.g., Shallow Landslide values summarized to reaches at the scale of drainage wings and then routed downstream) or to not reset at lakes. For example,as an index of erosion and sediment yield potential (rather than just an index of slope stability hazards), then sediment routed downstream will become intercepted by lakes, and thus a user might want to use the "reset values at lakes" option. Then a user imports the data (4) and the tool automatically routes the data to individual stream segments (a fish eye view of erosion potential) and then downstream.
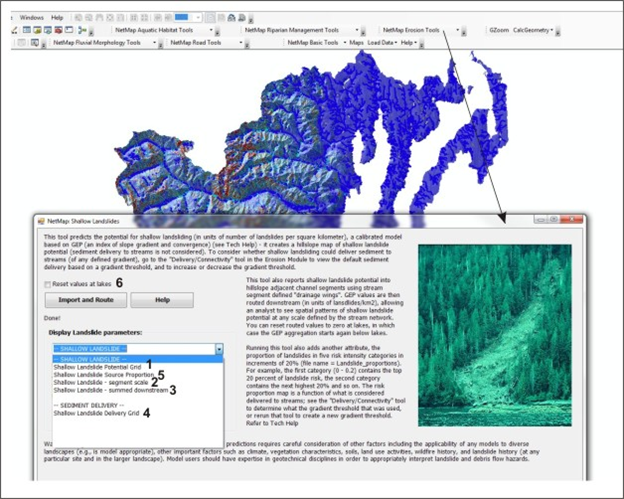 Figure 4. Once the Shallow Landslide Potential data have been imported, seven types of attributes are available for display: (1) the hillside prediction (Grid), without delivery, (2) the in-stream value (accumulated from both sides of the channel, via Drainage Wings, (3) the downstream routed or aggregated values, (4) landslide potential (grid) that can delivery sediment and organic material to the stream (which can be adjusted based on a channel gradient threshold [see Delivery Tool]), (not shown in list) the segment scale and aggregated values of the delivered shallow landslide potential, and (5) Shallow Landslide Risk Proportions (the proportion of landslide potential starting with the highest, in increments of 20%, e.g., the highest 20%, next highest 20% and so on). (6) Reach scale Shallow Landslide values can be routed (after the first time when it was done automatically) and values can be reset at lakes if required. Note, a similar shallow landslide index, GEP, can be used to make sediment yield predictions (t/km2/yr).
The resulting raster file provides a map of potential for sediment delivery (to a stream) for every pixel cell in a basin. The probability of sediment delivery is then multiplied by the shallow Landslide Intensity value, thus providing a prediction of sediment delivery (Figure 2).
As with any model, predictions of slope failure potential are “coarse grained” and thus approximate. Users are advised to validate predictions in the field and not to rely on the maps alone. However, NetMap’s shallow landslide intensity can be used as an effective screening tool at watershed scales, indicating where in a watershed the topography is most prone to failures, all other things being equal (Figure 5).
 Figure 5. A comparison between Generic Erosion Potential (top) and empirically calibrated shallow landslide potential (bottom). Predicted shallow landslide intensity provides additional information on the non uniform relationship between numbrs of landslides per unit area and topographic controls of failure (Figure 6).
Background
Individual landslide sites in the landslide inventory were geo-spatially referenced on 10-M DEMs and hence the slope gradients associated with failure sites were derived from the DEM (and not from the field measurements) since the goal was to develop a model that utilized a digital database. Consequently, the predicted locations of potential landslide sites (indexed by a variable landslide density) may occur on lower gradient areas (on the DEM), compared to what may be found in the field. In other words, 10-m DEMS commonly underestimate slope gradients. Hence, it is not appropriate to contrast a DEM-based slope gradient map with the predicted landslide density index to compare or contrast slide potential. A slope map can be used as a stand- alone measure of erosion potential, with the understanding that 10-m DEMs underestimate slope gradients. Likewise, the 10-m DEM-based landslide density predictions are a stand-alone representation of shallow failure potential, although the slope gradients associated with failure (on the DEM) are likely less than the gradients that would be measured at those locations in the field.
The model utilized 25-m satellite imagery of forest vegetation (Ohmann and Gregory 2002) that affects landslide density. Younger forests (post clearcut harvest) yield higher landslide rates because of the lower rooting strength compared to mature forests. However, landslide susceptibility in NetMap is predicted using mature forest cover to provide information on the intrinsic potential. Calculations are made at the resolution of the 10-m DEM, which for available USGS-provided data, reflects 40-foot contours mapped at 1:24,000 scale. Because of the empirical calibration, the model is best suited for coastal Oregon, although it should have applications for other mountain landscapes that are prone to shallow failures concentrated in steep and convergent areas. In other areas, the shallow landslide potential parameter is best used as a relative index (high – low).
To get an empirical estimate of landslide-initiation susceptibility, we use landslide density, that is, the number (or area) of landslides per unit land area (e.g., 1.2 landslides per km2, or 536 m2 landslide area per km2). Landslide density is based on the observed number (or area) of mapped landslides. Landslides tend to occur in certain types of locations. For example, translational failure of shallow soil layers – the type of landslide that tends to trigger debris flows in the Pacific Northwest – tend to occur on steep slopes (e.g., Sidle and Ochiai 2006). Such landslides do not occur in low-gradient terrain, and the number of landslides per unit area (landslide density) varies with slope steepness (e.g., hillslopes with gradients between 50% and 60% may have 0.4 landslides per km2, whereas slopes with gradients between 60% and 70% may have 0.8 landslides per km2). One may also look at how landslide density varies with other topographic attributes (contributing area, convergence), and with land cover, soil or rock type, vicinity to a road, rainfall intensity, and so on, but for now we focus on topographic attributes. So to define a spatially distributed estimate of landslide density, we overlay digitized landslide locations on topographic attributes derived from a digital elevation model (DEM).
For example, suppose we have mapped 100 landslides within a 100 km2 watershed, and our DEM-derived slopes show that areas with gradients between 60% and 70% cover 5 km2, and 25 of the mapped landslides lie in those areas. Then those slopes contain 25% of the mapped landslides, cover 5% of the watershed area, and have a landslide density of 4 landslides per km2. Moreover, to assess landslide potential, we assume that in the future, 25% of the landslides that occur in the watershed will, averaged over time, occur on those slopes. We perform the same exercise for every slope class. Each class then has a known landslide density, contains a known proportion of the landslides, and covers a known proportion of the watershed area. The landslide-density calibration for the Oregon Coast Range that we are currently using is shown in Figure 6. Rather than slope gradient alone, we use gradient weighted by a measure of topographic convergence, which for our calibration data better resolves landslide terrain than slope gradient alone (in that a larger proportion of the landslides are included in a smaller proportion of the area). Lacking a better term, we call this quantity a topographic index. Other types of topographic indices may also be defined. In our 2007 paper, for example, Kelly Burnett and I used slope and contributing area, based on the simple model proposed by Montgomery and Dietrich (1994).
 Figure 6. A non linear relationship exists between number of landslides or more specifically landslide density (number/km2, right panel) and the topogrpahic controls of failure (e.g., topographic index). Although the data are from the Oregon Coast Range, the non linear relationship likely holds in many landscapes. This allows the Landslide Intensity parameter to be applied to other landscapes prone to shallow failure, although as a relative index.
Model Description (2/3): Shallow Landslide Potential - Delivery to Streams Included
Field Name: LS_DEL_GRID; Common name: Landslide-delivery
To calculate the potential for sediment delivery to streams (from predicted shallow landslide areas), the model traces the down slope flow path from every pixel until it intersects a stream (similar to the Generic Erosion Potential [GEP] parameter). The calculated probability for sediment to be transferred to each downslope cell decreases monotonically as a function of gradient and topographic convergence. [Sediment delivery applies to mass wasting sediment delivery, say by debris flow or landslide. It does not apply to surface erosion processes, which is handled by the WEPP surface erosion model.] The probability that sediment will reach a stream is assigned to the source cell. This is repeated for all hillslope pixels. The predicted delivery of landslides to stream channels is based on a channel gradient threshold. For example, the Delivery Tool is used to estimate delivery potential to channels with a gradient equal to or less than 5%, 8% or 30% etc. (Figure 6).
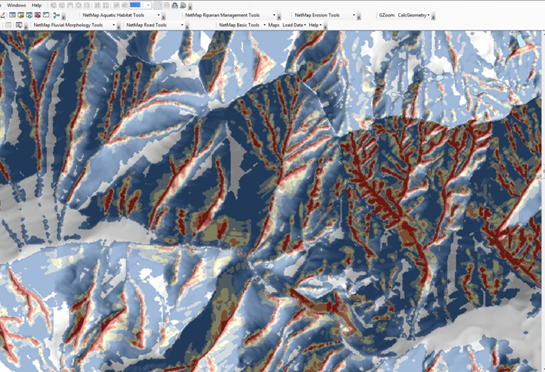 Figure 7. NetMap contains a tool for predicting the sediment (and wood) delivery to stream channels. Although the datasets are created using a default channel gradient threshold, a user can recalculate sediment delivery based on a new channel gradient threshold (i.e., 5%, 10%, 20% etc.).
Model Description (3/3): Shallow Landslide Intensity-Proportional Risk Assessment
Field Name: LS_PROP_GRID; Common name: Shallow Landslide Source Proportion
Another component of the shallow landslide analysis in NetMap, is the ability to represent landslide potential as proportions of risk. Starting with the highest to lowest predicted shallow landslide density, the tool identifies those areas with the highest 20% of predicted landslide risk, then the next highest 20% of risk, and so on. Thus, in Figure 8, the red colors represent those areas with the highest 20% of landslide risk (pixel values), the yellow the next 20% and so on.
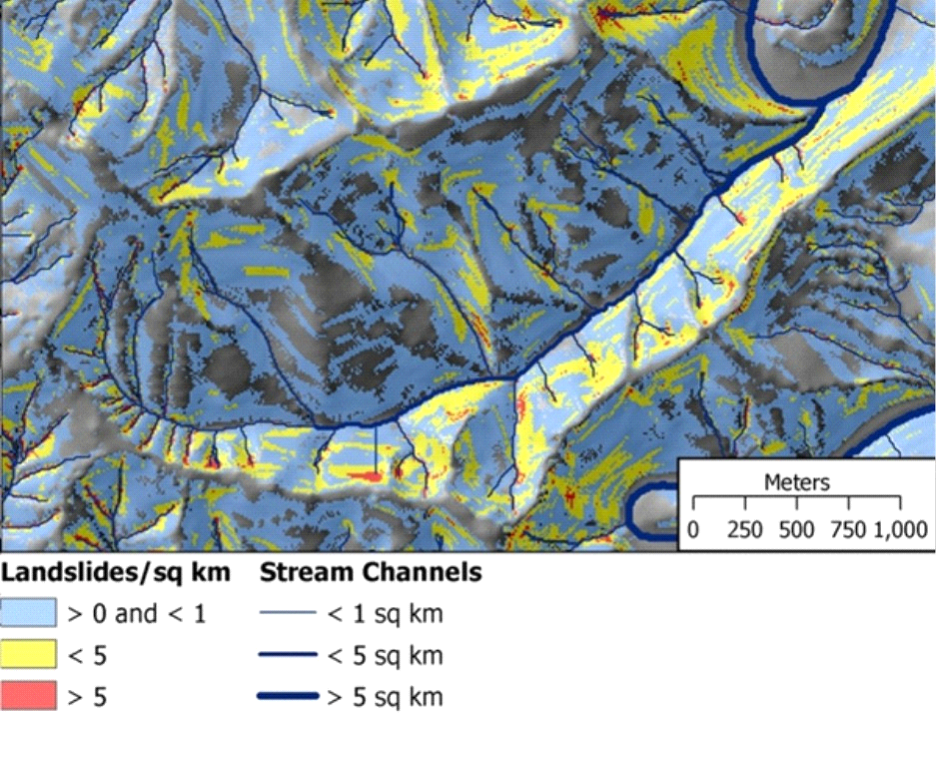 Figure 8. Proportions of landslide risk across a landscape in increments of 20%, starting with the highest 20% (in red). Note that the delivery component (based on a threshold receiving channel gradient) does NOT apply with this attribute. In addition, the mapped distribution of risk categories is sensitive to the area that is examined and the types of topography within it. For example, running the analysis in a small area with very low instability will yield one type of distribution and map, and running it over a larger area with a mix of stability (low to high) will yield another – by default, we are running it at the scale of NetMap datasets (approximately 500,000 acres).
More Background:
There are a variety of models available to predict shallow landslides, primarily for humid mountain landscapes (Sidle 1987, Montgomery and Dietrich 1994, Pack et al. 1998). Most models require information on hillslope topography, including gradients and some measure of convergence. Topographic information provided by 1:24,000 scale mapping does not resolve all topographic features pertinent to landslide locations (Benda and Dunne 1997). For instance, the landslide model does not account for small streamside failures (often referred to as inner gorge landslides) because of the inability of 10-m DEMs to resolve low relief landforms. Mapped landslide potential may also not resolve all small convergent areas, important to project level site-specific assessments. However, mapped landslide potential resolves topographic controls over larger areas, such as the relative risk between different first-order basins or between larger watersheds.
Slope gradient provides a basic topographic index for which relative landslide densities can be calculated. Other options include the SHALSTAB model [Dietrich and Montgomery, 1998] and the product of slope and local drainage area (that within a 10-m radius). For this project, we used the later, because it provided the greatest resolution of mapped landslide locations, in that it requires the smallest proportion of the study-site area to encompass a given proportion of all mapped landslide initiation points (Miller and Burnett 2007a).
The landslide density model allows for a somewhat finer grained resolution of landslide potential (intensity) compared to Generic Erosion Potential (GEP) (Figure 5). Although it also focuses on slope gradient and convergence, landslide density values reflect a topographic weighting that is calculated according to a comprehensive shallow landslide inventory. The landslide density predictions (#/km2) pertain specifically to the magnitude of the storm represented in the landslide inventory. For instance, the landslide density is what would be expected during another identical storm. Since there are many storms that can trigger landslides, we recommend that landslide density be used as a relative index (from high to low), although the specific numerical values for landslide density are available in the legend editor and can be displayed if desired. Specific landslide density values to create fixed categories of landslide potential (reflected in the different color codes) can be created to allow comparison across diverse watersheds.
The example mapping of landslide density in the northeastern portion of the Wilson and Trinity River watersheds reveals significant spatial variability. Such maps can be used as a screen by field foresters and geotechnical specialists. Use of generic erosion potential and landslide density predictions can be used to learn how to identify landslide prone areas in the field and from aerial photography (e.g., Figure 1).
Landslide Initiation
The first component, hillslope sources of debris flows, is based on a landslide model by Burnett and Miller (2007), described elsewhere in NetMap’s Technical Help. To summarize, the parameter of ‘landslide intensiy in the model is a multiplier of a landscapes average landslide density (e.g., 1.2 landslides per km2, or 536 m2 landslide area per km2). Landslides tend to occur in certain types of locations. For example, translational failure of shallow soil layers – the type of landslide that tends to trigger debris flows in the Pacific Northwest – tend to occur on steep slopes (e.g., Sidle and Ochiai 2006). Such landslides do not occur in low-gradient terrain, and the number of landslides per unit area (landslide density or intensity) varies empirically with slope steepness (e.g., hillslopes with gradients between 50% and 60% may have 0.4 landslides per km2, whereas slopes with gradients between 60% and 70% may have 0.8 landslides per km2).
Rather than slope gradient alone, a gradient weighted by a measure of topographic convergence, is used to better resolve landslide terrain than slope gradient alone (in that a larger proportion of the landslides are included in a smaller proportion of the area) (Miller and Burnett 2007), based on an approach proposed by Montgomery and Dietrich (1994). An example of predicted landslide density is shown in Figure 8.
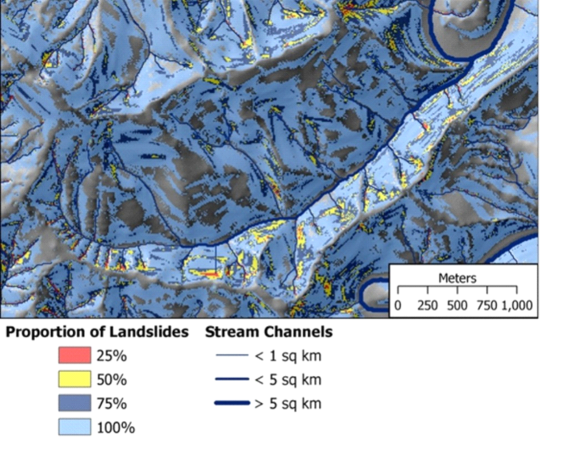 Figure 9. Landslide Intensity (e.g., multiple of average landslide density) is predicted for Lake Creek in the Oregon Coast Range. Extensive areas have a low predicted density with large values confined to steep slopes and bedrock hollows.
To obtain a value more readily interpreted in terms of relative landslide susceptibility, landslide density is converted to proportion of landslides, area weighted. Using slope-classes, the areas in specific slope steepness-area class are multiplied by landslide density. For example, suppose we have mapped 100 landslides within a 100 km2 watershed, and our DEM-derived slopes show that areas with gradients between 60% and 70% cover 5 km2, and 25 of the mapped landslides lie in those areas. Then those slopes contain 25% of the mapped landslides, cover 5% of the watershed area, and have a landslide density of 4 landslides per km2. Moreover, to assess landslide potential, we assume that in the future, 25% of the landslides that occur in the watershed will, averaged over time, occur on those slopes. We perform the same exercise for every slope class. Each class then has a known landslide density, contains a known proportion of the landslides, and covers a known proportion of the watershed area.
Classes are ordered in terms of decreasing landslide density, the number of landslides in each class (going from least stable – highest density – to most stable – lowest density) are summed to arrive a cumulative total, and then divide by the total to get a proportion. This provides a means to delineate areas in terms of an easily interpreted measure of landslide potential. If we want to delineate the smallest area that includes 25% of all mapped landslides, we’d include all areas with a value greater than zero and less-than-or-equal to 0.25; if we want the smallest area that includes 85% of all landslides, we’d include areas with values greater than zero and less-than-or-equal to 0.85 (fieldname = initProp, for initiation proportion) (Figure 10). The patterns are similar as those shown for landslide density in Figure 9, but in terms of the proportion of (expected) landslides included in any delineated area.
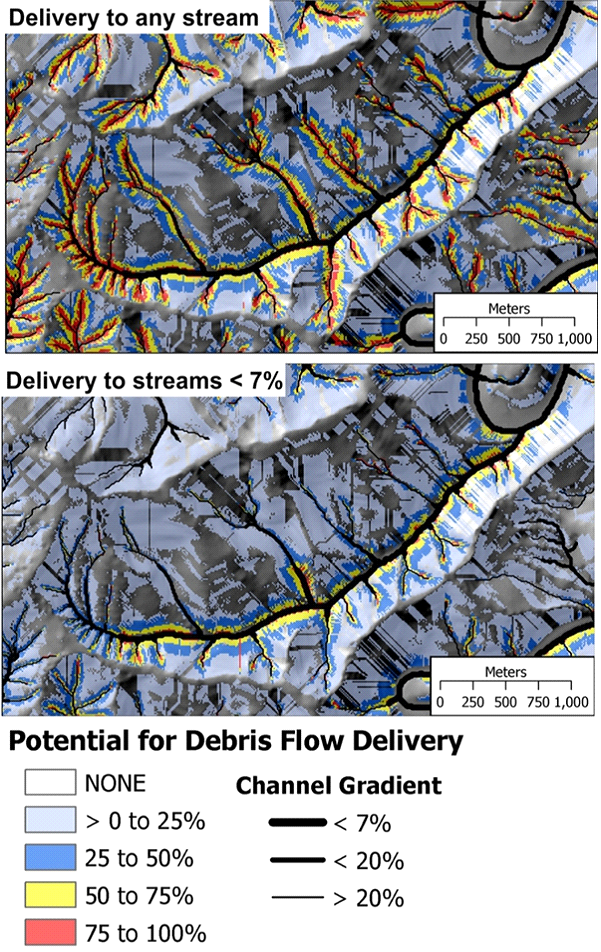 Figure 10. Shown are the areas encompassing a given proportion of expected landslides, starting with the least stable areas (in red). For example red zones cover 25% of the most unstable areas; red plus yellow cover 50% (including 25% of the next highest unstable areas); red, yellow, dark blue and light blue cover all expected landslide terrain. This illustrates the spatially variable nature of hillslope-channel connectivity with respect to mass wasting.
Connectivity or Delivery Potential
The next step in the model is to determine to what extent debris flows, triggered by shallow failures, can move downstream and enter large, fish bearing channels. A great many landslides never directly reach lower gradient (fish bearing) channels. Many landslides are small and don’t travel far (low connectivity); they do not carry wood to fish-bearing streams. Two debris flows initiating from the same shallow landslide location (perhaps separated in time by several centuries) will not necessarily travel the same distance. One may go a short distance, the other very far, depending on a variety of factors that we cannot quantify (e.g., how much material was stored in the debris-flow track, how large the initiating landslide was, how intense the triggering rainstorm was, etc.).
Our approach requires weighting each landslide initiation site by the probability that a debris flow triggered from that site travels to a channel of interest. To do that, we use the second empirical model (Miller and Burnett 2008). That model, as with the landslide model described above, uses a population of observed events as an indicator of future events. A set of mapped debris-flow tracks is used to quantify the influence of different landscape attributes – that can be measured using GIS data – on debris-flow-runout extent. Topographic attributes are chosen that are important controls on debris-flow behavior including runout track gradient and confinement, and attributes of channel junctions along the track (junction angle, gradient and confinement of the receiving channel). For additional detals, see Miller and Burnett 2008.
Based on the empirical database of mapped debris flows in the Oregon Coast Range (Robison, Mills et al. 1999), probabilities of debris flow scour or deposition were estimated using attributes obtained from the DEM (local gradient, confinement, etc.). Each point along each mapped track is characterized in terms of the cumulative upstream length of scour and deposition and the ratio of these lengths (length of deposition divided by length of scour) is calculated at the point where the debris flow stopped. For any particular value of the ratio, we can then see what proportion of the debris flows had a value that was larger at their terminus and what proportion had a value that was smaller. These proportions are used to estimate the probability. For example, along any potential debris-flow track we can calculate the ratio at all points. If, in our data, 20 out of 100 debris flows had ratio values less than 0.5 at their terminus, then we expect that, along any potential debris-flow track, there is a 20% chance that a debris flow traversing that track will stop upslope of that point (where the ratio of deposit to scour length is 0.5) and an 80% chance that it will stop downslope of that point.
From any potential debris-flow-initiation point, the flow path downslope, DEM-cell-by-DEM-cell, is used to calculate a probability (based on the proportions described above) that a debris flow continues past each cell along the way. We do this for every potential debris-flow-initiation site (every DEM cell with an estimated landslide density greater than zero from the previous model, e.g., Figure 8) and follow the runout path until it hits a channel of interest, or goes to zero. In this way, for every DEM cell, we can estimate the probability that a debris flow triggered from the cell travels to a point of interest (e.g., a fish-bearing stream) (Figure 11).
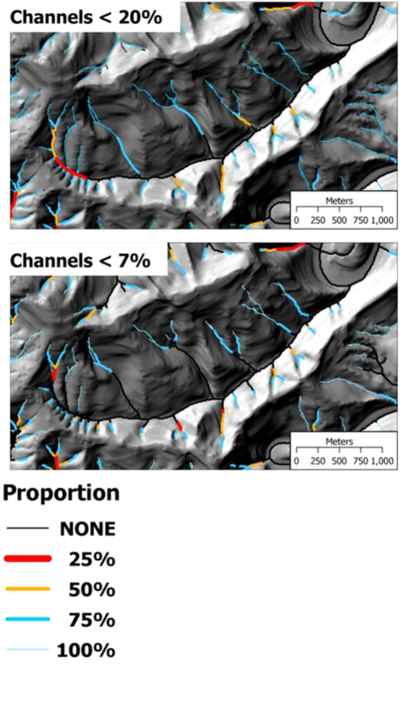
Figure 11. The upper map shows the predicted connectivity or the delivery potential of shallow landslides and debris flows (probability) for all streams in the Lake Creek tributary to the Alsea River in Coastal Oregon. The lower map shows the probability for delivery to a channel with gradient less than 7% (to approximate the portion of the channel network used by anadromous fish).
Landslide density (Figure 9) and probability for delivery (Figure 11) together provide a means to assess landslide potential from a stream-channel perspective. If we multiply the landslide density for each DEM cell by the probability for delivery, we get landslide density in terms of the number of landslides that deliver material to streams of interest (of a particular gradient threshold). We then use those values to translate landslide density to proportion of landslides, in this case, proportion of all landslides that deliver material to streams (Figure 12).
Figure 12. The predicted landslide density for each DEM cell is multiplied by the probability for delivery thereby creating a landslide density in terms of the number of landslides that deliver material to streams of interest (of a particular gradient threshold). Those values are translated into the proportion of all landslides that deliver material to streams.
The steps are as follows: use the initiation model (Figure 9, and see Shallow Landslide in Technical Help) to create a raster file of landslide density, the runout model to create a raster file of delivery probabilities (Figure 11), multiply the two to get a raster (grid) of delivery-weighted landslide density, and use this to generate the proportion-of-sources raster file. To reduce data-file sizes, values are aggregated to 5% bins and exported to a polygon shapefile, which is then used to generate maps to delineate source areas in terms of the proportion of debris flows that deliver, ranked from least to most stable.
Imagine standing in a low-order channels prone to debris flows. The contributing area to this point may contain many potential initiation sites, each one of which has some probability of generating a debris flow that will traverse the point you are standing, pick up the down wood buried beneath your feet, and continue downslope to a fish-bearing stream. We are interested in the likelihood that any of the upslope initiation sites will generate such a debris flow. For this, we interpret the delivery-weighted landslide density from each source DEM cell in terms of the probability that, in our calibration data set, a debris flow was generated from that cell and traveled downslope to a fish-bearing channel. This probability is based solely on the topographic attributes described above. We calculate the probability that such a debris flow didn’t happen, because we can estimate the probability that there were no debris flows from any of the upslope sources by multiplying the probability of non-occurrence over all sources. The probability that a debris flow did occur is then just one minus the probability that none did. We compute this for every DEM cell. So, based on our calibration data set, we estimate the probability for every DEM cell that it was traversed by a debris flow from upslope that continued downslope to a fish-bearing stream. The magnitude of these values is dependent on the number of debris-flow tracks included in our calibration data, so we need a way to normalize.
If we multiply this probability of traversal by flow length through the cell, and sum over all cells, we should get a value equal roughly to the total mapped track length of debris flows that traveled to fish-bearing streams in the calibration data set. We can, therefore, normalize these values in terms of the proportion of expected debris-flow track length. To do this, we rank cells by probability of traversal, multiply each by flow length through the cell, and sum (from largest probability to smallest) to get a cumulative travel length. We divide the cumulative length by the total sum to get a proportion (field name = trav). We calculate a value for every DEM cell. High trav values identify debris-flow corridors to fish-bearing streams.
So far, we’ve been working with raster data. To translate trav values to the vector channel-reach layer, the proportion of the expected debris-flow track length associated with any channel reach is obtained by summing trav values over the cells crossed by that reach. We assume that the calibration data is indicative of future events, so to delineate the smallest portion of the channel network within which a specified proportion of future debris-flow tracks will occur, we flag all channel reaches with an average trav value greater than zero and less than or equal to the proportion of interest. Examples for Lake Creek are shown in Figure 13.
 Figure 13. Low order channel, debris flow corridors to fish bearing streams in terms of channels to include in a given proportion of total debris flow track length. Channels of interest are defined in terms of a gradient threshold (<20%, <7%). The proportion is defined over the entire Alsea watershed, of which Lake Creek (shown) is only a small part.
Example Application
The foregoing discussion and modeling can be used to consider hillslope-channel connectivity more generally or the potential for debris flows to couple to fish bearing streams or for considering wood delivery by debris flows. For example, to delineate the smallest area that includes 25% of all landslides that deliver material to fish-bearing streams (based on the model), you would flag all areas with initProp values greater than zero and less than 25%. Note, we are not referring to 25% of the initiation sites (here, the DEM cells identified as potential landslide initiation sites), but to that collection of sites you must include to encompass 25% of the landslides that occur, which will typically entail much less than 25% of the sites. These sites are identified by the topographic attributes characteristic of locations where landslides were mapped in the calibration data set. Likewise, to identify the smallest proportion of the low-order channel network that includes 25% of all debris-flow track length (for those debris flows that traveled to fish-bearing streams), you would flag all channel reaches with trav values greater than zero and less than 0.25. To include all landslide sites that could trigger debris flows that travel to fish-bearing streams, and all low-order channels that could be traversed by a debris flow that travels to a fish-bearing stream, you would flag all areas with non-zero initProp values and all channels with non-zero trav values. The appropriate levels depend on the issue at hand.
Because we do not know a-priori which streams have fish and which don’t, and because some species persist further upstream than others, we provide results for two portions of the channel network:
1. All streams with no down-stream gradient greater than 20%, which corresponds roughly to the upper extent of fish use for all species. The DEMs used for the Oregon Coast Range are interpolated from 40-foot contour lines on 1:24,000-scale USGS topographic maps. To estimate channel gradient, we sum DEM-traced channel length between 40-foot contour-line crossings. Techniques used for tracing channels are described in Clarke et al. (2008).
2. All streams with no down-stream gradient exceeding 7%. This corresponds roughly to the upper extent of anadromous fish use.
The landslide-source areas indicated by initProp can be similar for each case; the proportional values found at any particular site vary between cases, but not as much as the relative change in delivery potential (except where delivery potential to low-gradient streams goes to zero, in which case, initProp also goes to zero). This may seem surprising; in general, the potential for delivery to a low-gradient stream (< 7%) is much lower than the potential for delivery to a high-gradient stream. This is clearly shown in the maps of delivery potential and of delivery-weighted landslide density. One might expect a similar change in initProp. Of the landslides that occur, there may be many that deliver material to the entire channel network, including steep channels, and not so many that travel all the way to low-gradient channels. The total number of landslides involved in each of the two cases is different, but with initProp, we are looking at relative values. The same source areas may be involved in each case, but the number of landslides that deliver to the channels of interest are different.
Likewise, the set of low-order channels identified as debris-flow corridors to fish-bearing streams is similar for both cases. We are dealing only with debris flows that continue downstream to fish-bearing streams. The probability that such a debris flow traverses any point in the channel network depends on the number of upslope debris-flow-initiation sources in the contributing area to that point. As we progress downstream, the contributing area increases and may include additional debris-flow-initiation sources. The potential for traversal by a debris flow (that continues to a fish-bearing stream), therefore, increases downstream (it cannot decrease) at a rate-per-unit-channel length dependent on the location of initiation source areas and the probability for delivery from each. Thus, the reaches with the greatest potential for debris-flow traversal are those at the downstream end of small, steep landslide-prone sub-basins tributary to the fish-bearing network. The downstream extent of these delineated channels is determined by our determination of the upstream extent of the fish-bearing network.
Because we are dealing with relative values, the patterns are dependent on the scale over which the analysis is performed. For example, a large watershed may have some sub-basins where the initProp value never exceeds 0.4. If we were to do the analysis over that sub-basin alone, it would, by definition, have values ranging up to 1.0. For NetMap, we do the analyses over each NetMap data set (roughly the size of a 4th-field hydrologic-unit-code basin).
|